Если ряд сходится, то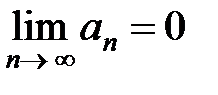 
.
Доказательство. Если ряд сходящийся, существует его конечная сумма 
, причем 
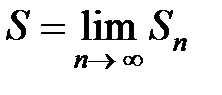. Вычислим
.
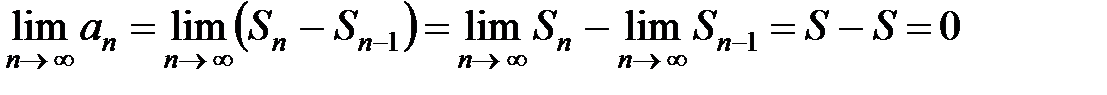Основное свойство рядов
Если ряд сходящийся, то его остаток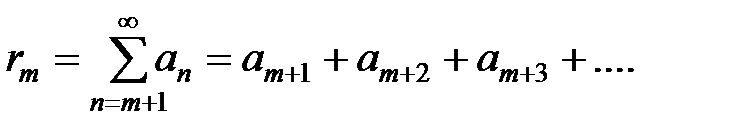 
, образованный отбрасыванием первых 
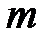членов ряда, тоже сходится. Если ряд расходящийся, то его остаток также является расходящимся рядом.
В самом деле,
.
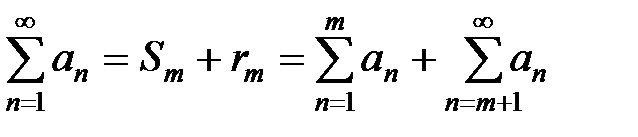Если ряд сходится, то существует его конечная сумма 
, а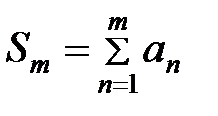 
- всегда конечна как сумма конечного числа членов. Тогда из 
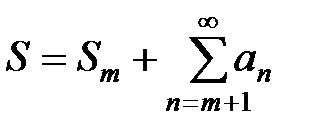следует, что 
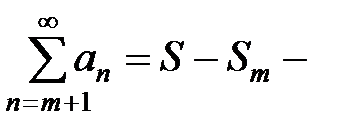конечное число, и остаток ряда – сходится. Когда ряд расходящийся, 
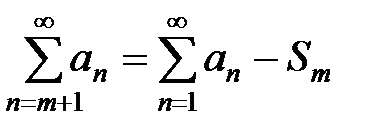. Поскольку сумма ряда в правой части равенства не существует (ряд расходящийся), а 
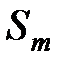имеет конечное значение, сумма ряда в левой части также не существует.
Переходим к рассмотрению частных случаев рядов. Вначале исследуем сходимость числовых рядов.
