Понятие обратной матрицы определено только для квадратных матриц, определитель которых не равен нулю. Если D=0, то заданная матрица обратной не имеет и называется особенной (или вырожденной).
Матрица А 
называется обратной по отношению к матрице А, если выполняется равенство: А А=АА =Е.
Алгоритм вычисления А покажем на примере А= 
по шагам:
1. Вычисляем определитель D= 
. Если D=0, то работа прекращается с заключением: А- вырожденная матрица.
2. Вычисляем все адъюнкты матрицы А: А 
=Ad , A 
=Ad , ... A 
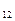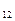=Ad 
.
3. Из вычисленных адъюнктов составляем союзную (или присоединенную) матрицу Ас= 
. Обратим внимание, что индексы этой матрицы транспонированы по отношению к исходной матрице А.
4. Вычисляем обратную матрицу А = 
Ас
5. Если расчет проводится вручную, то выполняется проверка: А А= Е или AA =Е.
Перечислим основные свойства обратной матрицы:
· D(A )= 
.
· (АВ) =В А , т.е. при раскрытии скобок порядок сомножителей меняется на обратный.
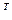· (А 
) =(А ) 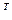, т.е. операции обращения и транспонирования можно менять местами.
В заключение отметим, что из-за арифметического объема работы с определителями, использование описанной процедуры ограничивается матрицами второго и третьего порядков.
