Так же,как в определителях, транспонирование - это замена строк столбцами: еслиА 
= 
, то А 
=. 
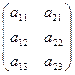
Приведем основные свойства транспонирования, которые легко доказываются вычислением:
· Двойное транспонирование возвращает исходную матрицу:
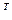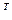(А 
) =А.
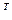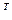· Транспонирование суммы матриц эквивалентно сумме транспонированных слагаемых: (А+В) =А +В .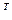
· Транспонирование произведения двух матриц эквивалентно произведению транспонированных матриц, взятых в обратном порядке:
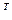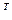(АВ) =В А .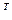
· Произведение матрицы на свою транспонированную: А 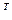А или АА 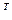всегда имеет результатом симметричную квадратную матрицу.
· Если матрица А- квадратная, то значение ее определителя не зависит от транспонирования: D(A)=D(A ).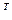
