· Две матрицы А и В равны, если они имеют одинаковую размерность и a 
=b , т.е. равны соответственно расположенные элементы.
· Две матрицы одинаковой размерности можно суммировать: С=А+В, причем результатом будет поэлементная сумма: с =а +в :
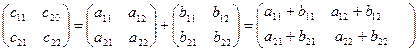
· Матрицу любой размерности можно умножить на число 
. Это значит - умножить на это число все элементы матрицы: 
А= (а )=( а )
· Матрицу А 
можно умножить на матрицу В 
тогда и только тогда, когда число столбцов у А, т.е. n, равно числу строк у В. Результатом будет матрица С 
. Элемент с этой матрицы равен сумме произведений элементов строки № i в матрице Ана элементы столбца № j в матрице В.Примеры:
= 
;
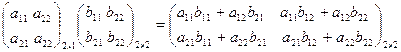
Несколько матриц множим по очереди: А 
В С 
=(АВ) С=D 
.
Отметим, что, в отличие от числовой арифметики, матрицы редко подчиняются правилу АВ=ВА. Чаще всего АВ 
ВА, если такая перестановка в принципе возможна. В немногих случаях, когда равенство соблюдается, Аи Вназываются коммутирующими матрицами. Особого практического значения они не имеют.
