Определение 2.Функция 
называется выпуклой на отрезке 
, если 
выполняется неравенство Йенсена 
.
Пример.Покажем, что функция 
является выпуклой на всей числовой оси. Пусть 
.
Рассмотрим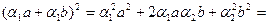 
.
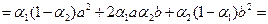
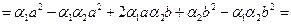
Таким образом, 
.
Определение 3.Функция называется выпуклой на отрезке , если 
касательная, проведенная к графику функции в точке с абсциссой 
, проходит не выше хорды, стягивающей точки с координатами 
и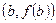 
. (Рисунок)
Определение 4.Функция называется вогнутой на отрезке , если выполняется неравенство 
.
Замечание.Выпуклость функции называют выпуклостью вниз, а вогнутость – выпуклостью вверх.
