Для того, чтобы функция 
, дифференцируемая на интервале 
была выпуклой на нем, необходимо и достаточно, чтобы 
монотонно возрастала на этом интервале. При этом строгому возрастанию соответствует строгая выпуклость 
.
Доказательство:
Необходимость. Пусть дифференцируема и выпукла на интервале . Тогда из определения выпуклости имеем, что 
, 
, 
, 
;
, 
; 
, 
. Так как 
то 
,
,
,
,
,
,
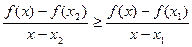. По теореме Лагранжа 
, где 
.
Таким образом, монотонно возрастает.
Достаточность. Пусть монотонно возрастает на интервале . Тогда по теореме Лагранжа 
, 
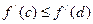, так как
, 
■
