Если функция 
в некоторой окрестности точки 
имеет разложение по формуле Тейлора, то это разложение единственно.
Доказательство:
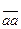. Пусть функция имеет два разложения:
,
.
Вычтем одно из другого и получим:
.
Пусть 
, тогда 
. Разделим полученное равенство 
на 
. Получим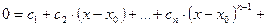 
. Тогда при получим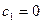 
. Рассуждая аналогично, получим 
. Следовательно, 
. Таким образом, разложения совпадают. ■
Замечание.Обратное утверждение, вообще говоря, неверно, т.е. можно найти такие две функции, которые будут иметь одинаковые разложения по формуле Тейлора в некоторой окрестности точки .
