Можно заметить, что чем больше производных совпадают у двух функций в некоторой точке, тем лучше эти функции аппроксимируют (приближают) друг друга в окрестности этой точки. Нас будет интересовать приближение функции в окрестности одной точки с помощью многочленов. Рассмотрим многочлен степени 
: 
. Заметим, что 
. Так как 
, то
. Аналогично получим 
,
.
Определение 1.Функция 
называется гладкой порядка 
в точке 
на интервале 
, если она имеет все производные порядка включительно, причем эти производные являются непрерывными функциями на отрезке 
. Этот факт обозначается 
.
Определение 2.Выражение вида 
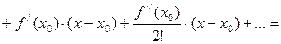
называется формулой Тейлора для функции 
в окрестности точки .
Теорема 1.Если функция является гладкой порядка в некоторой окрестности точки , то имеет место формула Тейлора для данной функции .
Доказательство:
Пусть имеет место формула Тейлора для функции : 
, причем
, 
, 
. Обозначим
.
Используя правило Лопиталя, покажем, что 
. Так как 
, …, 
, 
,
тогда 
=
=…= 
. ■
Замечание.В формуле Тейлора первое слагаемое называют главной частью функции, а второе – остаточный член функции .
Если 
, то формулу Тейлора 
для функции называют формулой Маклорена.
Остаточный член в виде 
называют остаточным членом в форме Пеано.
Формула Тейлора используется для того, чтобы приблизить функцию многочленом 
-й степени в некоторой окрестности точки 
: 
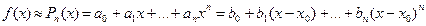
Пример.Разложим многочлен 
по степеням 
. Для этого найдем коэффициенты разложения: 
, 
,
, 
. Тогда
.
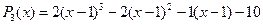