Пусть функции 
и 
непрерывны и дифференцируемы в некоторой проколотой окрестности 
точки 
, причем 
, 
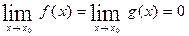и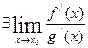 
. Тогда 
.
Доказательство:
Рассмотрим окрестность . (Рисунок) Выберем последовательность 
. Тогда, начиная с некоторого номера N, члены последовательности попадают в эту окрестность. Тогда, так как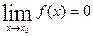 
и 
, то функции и в точке имеют устранимый разрыв. Доопределим эти функции до непрерывности: 
, 
. Тогда на отрезке 
данные функции непрерывны и дифференцируемы на интервале 
. Таким образом, выполняются все условия теоремы Коши. Это значит, что
, где 
, или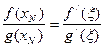 
.
Перейдем к пределу при 
: 
,
. ■
Замечание.Если 
не существует, то из этого не следует, что не существует 
.
Пример.Вычислим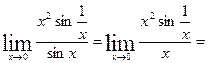 
, но 
не существует.
Пример.Вычислим 
. Применяя правило Лопиталя, получим 
.
Замечание. Теорема Лопиталя сформулирована для неопределенности типа 
и имеет место для неопределенностей типа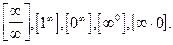 
Пример.Вычислим 
. Для этого прологарифмируем функцию 
. Тогда 
. Следовательно, 
.
