Теорема 3. Теорема Коши

Пусть функции и непрерывны на отрезке и дифференцируемы на интервале , причем . Тогда такая, что .

Доказательство:

Докажем сначала, что . Функция удовлетворяет условиям теоремы Лагранжа, значит, что . Отсюда .

Введем вспомогательную функцию так, чтобы она удовлетворяла условиям теоремы Ролля.

.

Тогда . Отсюда

.

Таким образом,

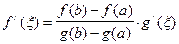или . ■

Замечание.Теорема Коши является наиболее общей теоремой, т.е. теорема Ролля и Лагранжа являются следствиями из теоремы Коши.