Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале  , тогда найдется точка
, тогда найдется точка  .
.
Доказательство:
Введем вспомогательную функцию  так, чтобы функция
так, чтобы функция 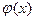 удовлетворяла теореме Ролля, т.е.
удовлетворяла теореме Ролля, т.е.  :
:
 ,
,  ,
,
 .
.
Тогда  ,
,
 ,
,  . Таким образом,
. Таким образом,  ■
■
Замечание. Геометрический смысл теоремы:
$ точка x, в которой касательная к графику функции имеет такой же наклон, как и хорда, соединяющая точки  и
и 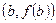 . (Рисунок)
. (Рисунок)
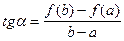 .
.
Замечание.Теорема Лагранжа является обобщением теоремы Ролля.
Следствие 1. Формула конечного приращения
Если  то
то 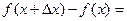
 где
где  , или
, или  .
.
Следствие 2. Критерий монотонности
Для того, чтобы функция  , непрерывная на отрезке
, непрерывная на отрезке  и дифференцируемая на интервале
и дифференцируемая на интервале  , была неубывающей (невозрастающей), необходимо и достаточно, чтобы
, была неубывающей (невозрастающей), необходимо и достаточно, чтобы  .
.
Доказательство:
Необходимость. Пусть функция  не убывает на отрезке
не убывает на отрезке  . Тогда, по определению, имеем
. Тогда, по определению, имеем  . Возьмем любой
. Возьмем любой  и придадим ему положительное приращение
и придадим ему положительное приращение  . Получим
. Получим  .
.
Достаточность. Пусть 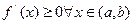 . Возьмем точки
. Возьмем точки  такие, что
такие, что  и применим теорему Лагранжа:
и применим теорему Лагранжа:  , где
, где  . Тогда
. Тогда  или
или  . Таким образом, получили определение неубывающей функции. ■
. Таким образом, получили определение неубывающей функции. ■