Пусть 
непрерывна на отрезке 
и дифференцируема на интервале 
, причем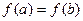 
.Тогда найдется точка 
.
Доказательство:
Так как функция непрерывна на отрезке , то по теореме Вейерштрасса она достигает своих наибольшего и наименьшего значений (ТВГ, ТНГ).
Пусть 
, а 
. Тогда возможны два случая:
1. Если 
, то 
. Тогда 
.
2. Если 
, то пусть 
. Это значит, что на интервале , по крайней мере, в одной точке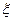 
функция будет иметь экстремум, а по теореме Ферма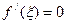 
. ■
Замечание.Все условия данной теоремы существенны. (рисунки – 3 шт.).
