Пусть функция 
непрерывна на отрезке 
и дифференцируема на интервале 
, причем 
- точка локального экстремума функции . Тогда 
.
Доказательство:
Для определенности пусть 
- точка локального экстремума, т.е. 
. Рассмотрим производную 
.
Так как 
, то получим, что 
. ■
Замечание.Теорема Ферма является необходимым условием экстремума. Обратное утверждение, вообще говоря, неверно.
Пример.Рассмотрим функцию 
. Производная функции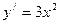 
равна нулю при 
, но эта точка не является точкой экстремума функции.
Пример.Для квадратичной функции 
абсцисса вершины параболы является точкой экстремума, а ордината 
- экстремумом функции. Исходя из этого, найдем координаты 
вершины параболы. Так как 
и 
, 
, то 
.
