Определение 2.Пусть для каждой точки и 
плоскости 
существует единственное число 
. Тогда говорят, что на плоскости задана функция 
двух переменных 
и 
.
Определение 3.Придавая постоянные значения числу z ( 
), получим уравнения, задающие линии в пространстве. Тогда функция 
, заданная уравнением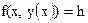 
, называется заданной неявно.
Для того, чтобы продифференцировать неявно заданную функцию , необходимо продифференцировать обе части уравнения .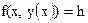
Пример. Если 
, то уравнение 
задает окружности с центром на оси 
. Найдем производную функции , заданной уравнением : 
.
