Для того, чтобы функция 
была дифференцируема в точке 
, необходимо и достаточно, чтобы в этой точке у нее существовала производная.
Доказательство:
Необходимость.Пусть дифференцируема в точке , тогда по определению ее приращение можно представить в виде: 
.
Найдем отношение приращения функции к приращению аргумента: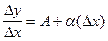 
. Перейдем к пределу: 
.
С другой стороны, этот предел равен 
, т.е. 
.
Достаточность. Пусть существует . Тогда по определению производной: 
. Это значит, что: 
. Умножив последнее равенство на Dx, получим: 
.
Полагая, 
, мы получили определение дифференцируемости. ■
Замечание.Процесс нахождения производной функции в точке называют дифференцированием.
Замечание.Производную 
называют правой производной функции 
в точке , а производную 
- левой производной.
Таким образом, 
, причем 
.
Теорема 2.Если функция 
дифференцируема в точке , то она непрерывна в этой точке.
Доказательство:
Пусть функция дифференцируема в точке . Тогда по определению . Найдем 
. Значит,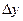 
является бесконечно малой функцией. Следовательно, функция непрерывна в точке . ■
Замечание.Обратное утверждение неверно. Например, функция 
непрерывна в точке 
, но не дифференцируема в этой точке.
Определение 3.Говорят, что функция дифференцируема на отрезке 
, если она дифференцируема в каждой внутренней точке этого отрезка.
