Заметим, что в – угол наклона хорды 
, где 
, а б - угла наклона касательной, проведенной к графику функции 
. Если 
, то 
. Это значит, что 
. Таким образом, значение производной функции в точке 
равно тангенсу угла наклона касательной, проведенной к графику функции в точке с абсциссой .
Физический (механический) смысл производной
Пусть точка движется по закону 
. Вычислим среднюю скорость движения за момент времени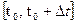 
: 
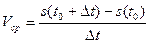. Устремим 
, тогда 
.
Таким образом, значение производной перемещения в момент времени 
равно мгновенной скорости движения точки в данный момент времени.
Рассмотрим функцию 
.
Тогда 
.
Пример. Рассмотрим функцию 
.
Тогда 
.
Пример.Рассмотрим функцию 
.
Тогда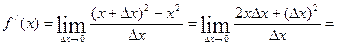 
.
Пример.Рассмотрим функцию 
.
Найдем значение производной данной функции при 
.
Так как 
,
, то производная этой функции в точке не существует. Более того,
функция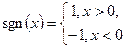 
является производной исходной функции при 
.
Определение 2.Пусть функция 
определена в некоторой окрестности точки 
, тогда называется дифференцируемой в этой точке, если приращение функции в данной точке представимо в виде:
, где 
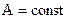и 
.
