|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Векторний добуток двохДата добавления: 2015-08-14; просмотров: 1020; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

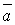 і
і 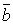 називається вектор
називається вектор 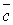 , який задовольняє таким умовам:
, який задовольняє таким умовам: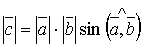 (37).
(37).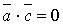 та
та 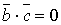 (38).
(38).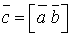 або
або 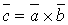 (39).
(39).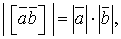 якщо
якщо 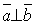 (40).
(40).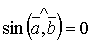 і векторний добуток їх дорівнює нуль-вектору, тобто
і векторний добуток їх дорівнює нуль-вектору, тобто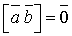 (41).
(41).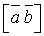 не виконується, або точніше вектор
не виконується, або точніше вектор 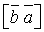 має напрям, протилежний до
має напрям, протилежний до 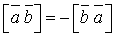 (42).
(42).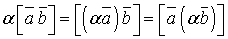 (43).
(43).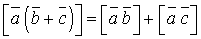 (44).
(44).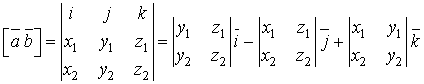 (45).
(45). є вектор сили, прикладеної до деякої точки В, а вектор
є вектор сили, прикладеної до деякої точки В, а вектор  , спрямований з точки А в точку В, то векторний добуток
, спрямований з точки А в точку В, то векторний добуток 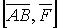 буде моментом
буде моментом 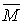 сили
сили 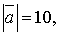
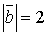 і
і 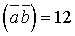 . Обчислити
. Обчислити 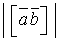 .
.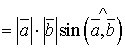 . Для того, щоб розв’язати задачу, нам потрібно знайти
. Для того, щоб розв’язати задачу, нам потрібно знайти 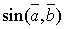 . З умови
. З умови 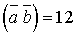 маємо:
маємо: 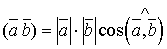 , звідки
, звідки 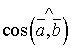 =
= 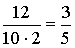 . Оскільки
. Оскільки 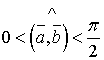 .
.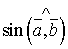 :
: 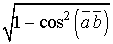 =
= 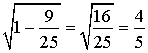 .
.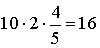 .
.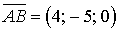 та
та 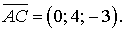 Тоді згідно з формулою
Тоді згідно з формулою 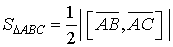 та формулою (45) дістанемо:
та формулою (45) дістанемо: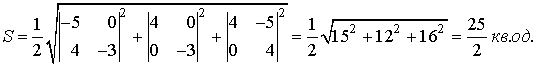
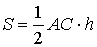 , тобто
, тобто 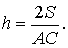 Отже, знаходимо
Отже, знаходимо 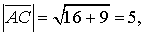 і маємо
і маємо 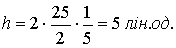
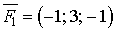 та
та 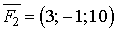 . Знайти момент рівнодіючої цих сил, його величину та напрямні косинуси відносно точки В(2; 4; 0).
. Знайти момент рівнодіючої цих сил, його величину та напрямні косинуси відносно точки В(2; 4; 0).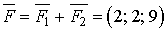 та вектор
та вектор 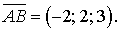 Згідно зі сказаним вище, момент сили знаходиться за формулою:
Згідно зі сказаним вище, момент сили знаходиться за формулою: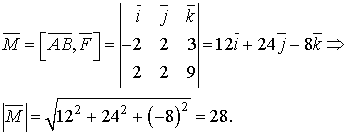
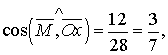
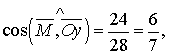
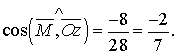
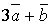 та
та 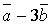 були колінеарними?
були колінеарними?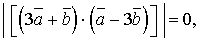
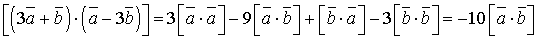 ,
,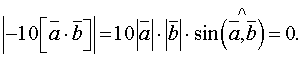
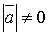 і
і 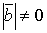 , отже
, отже 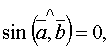 звідки
звідки 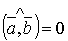 або
або 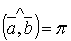 , тобто вектори
, тобто вектори  Довести, що
Довести, що 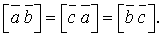
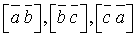 перпендикулярні до площини трикутника і всі вони спрямовані в один бік:
перпендикулярні до площини трикутника і всі вони спрямовані в один бік: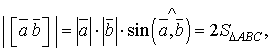
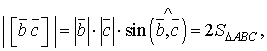
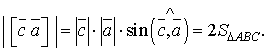
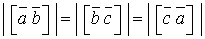 , тому що кожний з виразів дорівнює подвійній площі трикутника АВС. Таким чином, усі три вектори
, тому що кожний з виразів дорівнює подвійній площі трикутника АВС. Таким чином, усі три вектори