Нехай вектор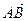 
складає кут 
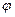з віссю 
.
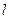Проекцією вектора 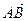на вісь 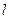називається число, рівне довжині вектора 
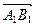(рис.1), взятої зі знаком «плюс», якщо напрям вектора 
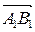збігається з напрямком осі і зі знаком «мінус» у противному випадку.
Проекцію вектора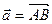 
на вісь 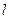можна обчислити за формулою:
.
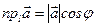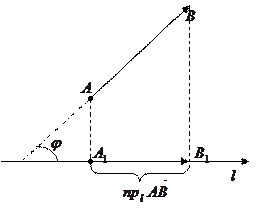
Декартовими прямокутними координатами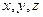 
вектора 
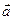називаються його проекції на відповідні координатні осі 
.
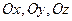Вектор 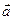з координатами 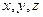записують у вигляді 
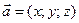або, 
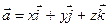де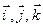 
- одиничні вектори координатних осей 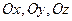відповідно. Довжина вектора 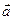визначається за формулою:
.
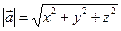Якщо вектор 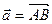заданий точками 
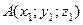і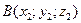 
, то його координати обчислюються за формулами:
.
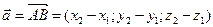Приклад 2. Дано дві точки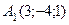 
і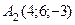 
. Знайдіть координати і довжину вектора 
.
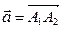За умовою задачі,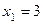 
, 
, 
, 
, 
, 
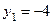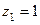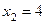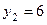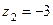. Значить, 
.
.
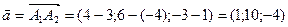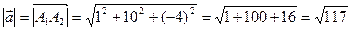Приклад 3. Дано два вектор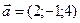и 
и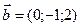 
. Знайдіть координати і довжину вектора 
.
; 
;
;
.
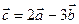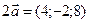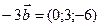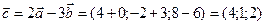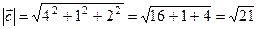Поєднаємо паралельним переносом початок деякого вектора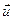 
з початком координат прямокутної системи координат 
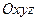. Нехай 
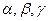- кути, які утворює вектор 
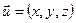з осями координат 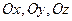відповідно (рис.2). Напрям вектора 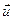визначається за допомогою направляючих косинусів 
, 
, 
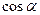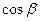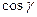, для яких справедливі рівності:
,
.
