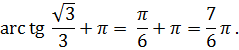Теперь вспомним арктангенс и обозначим его особенности.
Точки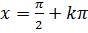 
(k —любое целое число) разделяют всю числовую прямую на интервалы, в каждом из которых тангенс возрастает и может иметь любое заданное действительное значение, или, как говорят условно, в каждом из рассматриваемых интервалов тангенс возрастает от -∞ до ∞. Следовательно, в каждом из интервалов 
возможен переход к обратной функции.
Определение. Функция, обратная функции 
в интервале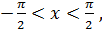 
называется арктангенсом:
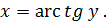
В геометрической терминологии это определение формулируется так (меняем местами 
и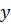 
): 
есть дуга, взятая в интервале от 
до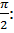 
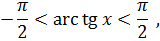
тангенс которой равен :
Примеры нахождения арктангенса:
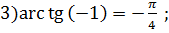
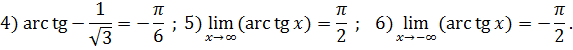
Перечислим основные свойства арктангенса.
1°. Функция 
в интервале 
возрастает от 
до (сами граничные значения 
исключаются). Это следует из монотонности и взаимной однозначности отображения друг на друга интервалов:
и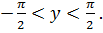 
2°. При изменении знака аргумента имеет место равенство:
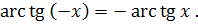
График арктангенса показан на чертеже 4.
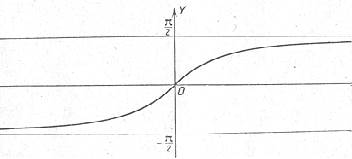
Черт.4
Примеры нахождения дуги с помощью арктангенса:
1. Найти дугу в интервале 
тангенс которойравен 
Имеем 
и 
Поэтому искомая дуга есть:
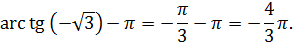
2. Найти дугу в интервале 
тангенс которой равен 
имеем 
и 
Искомая дуга есть
