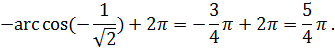Рассмотрим еще одну обратную тригонометрическую функцию — арккосинус и вспомним её свойства.
Определение. Функция, обратная функции  на сегменте
на сегменте  , называется арккосинусом:
, называется арккосинусом:
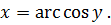
В геометрических терминах это определение формулируется так (меняем местами буквы  и
и 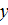 ):
):
 есть дуга, взятая в промежутке от
есть дуга, взятая в промежутке от  до
до  :
:

косинус которой равен  :
:
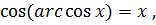
где 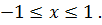
Областью определения функции  x является сегмент
x является сегмент  Если
Если  , то
, то  не имеет смысла.
не имеет смысла.
Рассмотрим примеры вычисления арккосинуса в разных точках:
1)  ; 2)
; 2)  ; 3)
; 3) 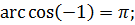
4) 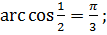
5)  6)
6)  7)
7)  8)
8)  не имеет смысла.
не имеет смысла.
Основные свойства арккосинуса:
1°. На сегменте  функция
функция  убывает от
убывает от  до нуля.
до нуля.
Это следует из того, что обратная функция  на сегменте
на сегменте  убывает от 1 до -1.
убывает от 1 до -1.
2°. Имеет место равенство:

График арккосинуса представлен на чертеже 3.

Черт. 3
Примеры нахождения дуги с помощью арккосинуса:
1) Найти дугу на сегменте  косинус которой равен
косинус которой равен 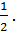
Искомой дугой является
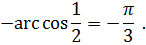
2) На сегменте  найти дугу, косинус которой равен
найти дугу, косинус которой равен 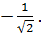
Имеем  и
и 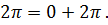
Решение задачи дает дуга