Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:
F' (x) = f(x).
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение - ∫ f(x) dx.
Неопределённый интегра́л для функции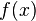 
— это совокупность всех первообразных данной функции.
Если функция 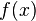определена и непрерывна на промежутке 
и 
— её первообразная, то есть 
при 
, то
,
где С — произвольная постоянная.
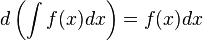
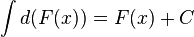
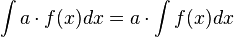
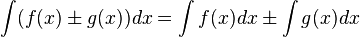
Если 
, то и 
, где 
— произвольная функция, имеющая непрерывную производную
