Первообрáзной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции 
называют такую 
, производная которой (на всей области определения) равна , то есть 
. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так, например, функция 
является первообразной 
. Так как производная константы равна нулю, 
будет иметь бесконечное количество первообразных, таких как 
или 
и т. д.; таким образомсемейство первообразных функции можно обозначить как 
, где 
— любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения .
Первообразные важны тем, что позволяют вычислять интегралы. Если — первообразная интегрируемой функции , то:
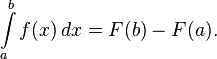
Это соотношение называется формулой Ньютона — Лейбница.
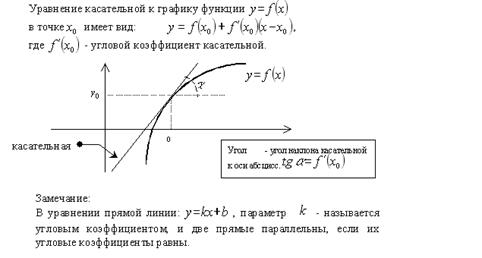
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
