Вектор-функция , определенная в некоторой окрестности точки , называется непрерывной в точке , если .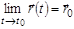
Из равносильности (1.4) и (1.7) следует, что для того чтобы вектор-функция была непрерывной в точке , необходимо и достаточно, чтобы в этой точке были непрерывны функции .
, определенная в некоторой окрестности точки 
, называется непрерывной в точке 
.
.