Предел вектор функции и его свойства

Пусть вектор-функция определена в окрестности точки , кроме самой точки .

Вектор называется пределом векторной функции при (или в точке ), если

. (1.4)

Если есть предел функции при , то это записывается так

. (1.5)

Если записать векторную функцию и вектор в проекциях

,

,

то получим

. (1.6)

Тогда из равенства (1.4) следует, что

, , . (1.7)

Свойства вектор-функции:

1. Если , то .

2. .

3. , − скалярная функция.

4.

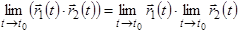
5. .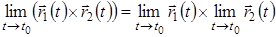