Выделяют следующие действия с числовыми рядами (они имеют смысл, т.е. сохраняют сумму ряда, только если она существует):
- Линейная комбинация рядов
Если ряды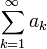 
и 
сходятся, то сходится и ряд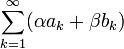 
(α, β — постоянные), при этом
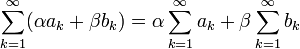
Сгруппируем слагаемые ряда 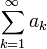, объединив без изменения порядка следования по нескольку (конечное число) членов ряда. Получим некоторый новый ряд . Раскрытие скобок в ряде в общем случае недопустимо, однако: если после раскрытия скобок получается сходящийся ряд, то раскрытие скобок возможно; если а каждой скобке все слагаемые имеют один и тот же знак, то раскрытие скобок не нарушает сходимости и не изменяет величину суммы.
Если ряд сходится абсолютно, то любой ряд, полученный из него перестановкой членов, также сходится абсолютно и имеет ту же сумму, что и исходный ряд. Если ряд сходится условно, то для любого наперёд заданного A (в том числе 
, 
, 
) можно так переставить члены этого ряда, что преобразованный ряд сходится к A (расходится к 
, 
, 
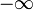) либо не имеет предела
