Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.
Суммой сходящегося числового ряда называется предел последовательности его частичных сумм, то есть, .
В нашем примере 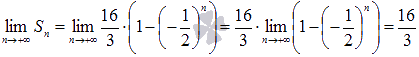, следовательно, ряд сходится, причем его сумма равна шестнадцати третьим: .
называется сходящимся, если существует конечный предел последовательности частичных сумм 
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд 
.
, следовательно, ряд 
сходится, причем его сумма равна шестнадцати третьим: 
.