Для сходимости ряда (1) необходимо и достаточно, чтобы для любого 
существовало число 
такое, что при 
и 
(n и p – натуральные числа) было выполнено неравенство
.
В частности, если ряд сходится, то 
.
Теорема : Если ряд 
сходится, то его общий член стремиться к нулю, т.е. .
Доказательство. По условию ряд
сходится. Обозначим через S его сумму. Рассмотрим частные суммы ряда 
и 
. Отсюда 
. Т.к. 
и 
при 
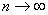, то
.
Условие является необходимым, но не достаточным условием сходимости ряда.
