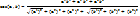Скалярным произведением двух векторов называют произведение их длин на косинус угла между ними.
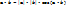
(a*b)– скалярное произведение.
---Скалярное произведение равно 0 тогда и только тогда, когда векторы ортогональны.
Свойства:
1)a*b = b*a (коммутативна)
2) 
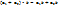(дестрибутивно)
3) 
(однородность скалярного произведения)
4)a*a>0
---Скалярным квадратом вектора называют скалярное произведение на себя.
---Скалярный квадрат вектора равен квадрату его модуля
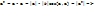
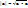
--Скалярное умножение одной линейной комбинации векторов на другую выполняют аналогично умножением одного многочлена на другой.
---Векторное пространство 
(аффинное пространство 
) в котором введено скалярное умножение векторов удовлетворяющая свойству скалярного произведения называют эквивалентным 
.
12. Скалярное произведение двух векторов в прямоугольных декартовых координатах.
Скалярное произведение двух векторов в прямоугольной декартовой системе координат равна сумме произведений соответствующих координат этих векторов.
1)Скалярный квадрат вектора равен сумме его координат.
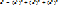
2)модуль вектора равен арифметическому квадратному корню из сумм квадратов его координат
2)модуль вектора равен арифметическому квадратному корню из сумм квадратов его координат.
---косинус угла между двумя векторами в ПДСК можно найти по формуле:
