Набор векторов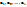 
называется системой вектроов
Система из k векторов 
называется линейно зависимой, если существуют такие числа 
, не все равные нулю одновременно, что:
Систему из k векторов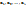 
наз-ся линейно независимой, если равенство (1.1) возможно только при 
, т. е. когда линейная комбинация в левой части равенства (1.1) тривеальная.
Замечание:
1.Один вектор a, тоже образует систему: при 
– линейно зависимую, а при 
линейно независимую.
2.Любая часть системы векторов называется подсистемой.
--Линейную комбинацию (1.1) векторов называют нетривеальной,, если хотя бы один из коэф-ов 
отличен от нуля. В противном случае, линейную комбинацию (1.1) называют тривеальной.
--Семейство векторов содержащий нуль вектор линейно зависим.
Векторы a+b колинеарны тогда и только тогда, когда векторы a и b линейно зависимы.
Векторы a, b, c кол-ны, то a, b, с лигейно зависимы.
