Ранее было показано, что в ряд Фурье разлагаются только периодические функции с периодом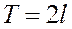 
или 
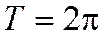, т. к. функци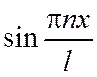и 
и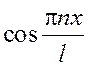 
периодические.
Если функция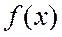 
не является периодической, то, чтобы разложить ее в ряд Фурье, строят некоторую периодическую функцию 
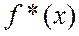, которая в области определения функции совпадает с функцией 
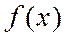. В этом случае говорят, что функцию 
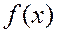периодически продолжают на всю числовую ось.
Возможны следующие случаи:
1. Если функция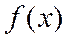 
задана на 
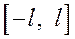, то строят функцию 
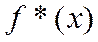с периодом 
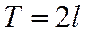. Она на отрезке 
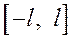совпадает с функцией 
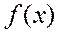, а на остальной части числовой оси является ее периодическим продолжением.
2. Если функция 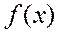задана на 
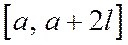, то строят 
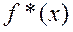с периодом 
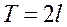, которая на отрезке 
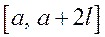совпадает с функцией 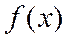и т.д. Коэффициенты Фурье будут находиться по известным формулам 1, только пределами интегрирования являются 
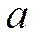и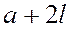 
.
3. Если функция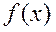 
задана на отрезке 
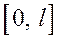, то для разложения в ряд Фурье достаточно ее доопределить на отрезке 
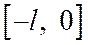произвольным способом. Затем разложить в ряд Фурье, считая ее заданной на отрезке 
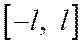. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках отрезка 
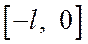находились из условия 
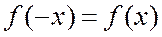или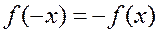 
. В первом случае функция 
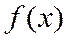на отрезке 
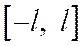будет четной, а во втором – нечетной. При этом коэффициенты разложения такой функции ( 
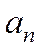в первом случае, 
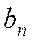– во втором) можно определить по вышеперечисленным формулам для коэффициентов четных и нечетных функций.
