Разложение периодической функции в ряд Фурье называется гармоническим анализом.
Рассмотрим слагаемые ряда Фурье.
Значение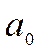 
равно среднему значению функции 
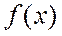на всей оси.
Первое непостоянное слагаемое называется основной гармонической, оно имеет период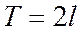 
.
Остальные слагаемые называются верхними гармониками, их наименьшие периоды равны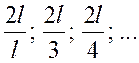 
Если независимая переменная рассматривается как время, то ряд Фурье описывает произвольное периодическое колебание в виде суммы гармонических колебаний с кратными частотами.
Например, в акустике: основное слагаемое определяет высоту звука, т. е. основной тон; остальные слагаемые описывают обертоны, от которых зависит тембр звука.
Ряды Фурье используются в решении задач математической физики, а также их применяют при изучении различных зависимостей в электрических цепях с несинусоидальными токами.
