Если функция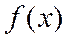 
четная на 
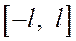, т. е. 
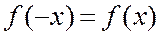, то график симметричен относительно оси 
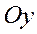, определенный интеграл рассматривается как площадь криволинейной трапеции.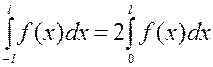 
Если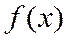 
нечетная функция на 
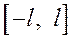, т. е. 
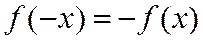, то график симметричен относительно начала координат. Получим 
.
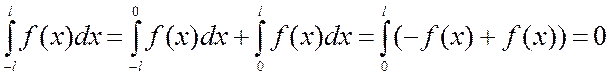Произведение двух четных или двух нечетных функций есть четная функция. Произведение четной и нечетной есть нечетная функция.
Тогда:
– если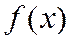 
– четная функция на отрезке 
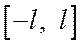, то 
,
, 
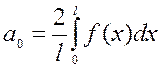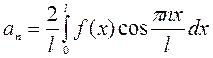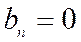,при этом функция разлагается в ряд Фурье только по косинусам 
;
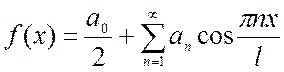– если 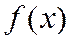– нечетная функция на 
, то 
,
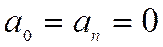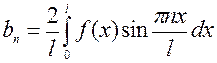, при этом функция раскладывается в ряд Фурье только по синусам 
;
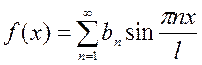– если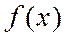 
ни четная, ни нечетная функция, то ее тригонометрический ряд Фурье содержит и синусы, и косинусы.
Пример.Разложить в ряд Фурье функцию, заданную на отрезке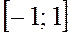 
уравнением 
.
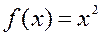Решение.
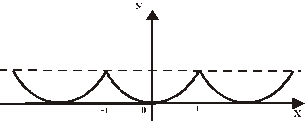
Рассматриваемая функция является четной, т. к.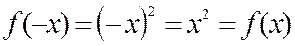 
. Ее график – дуга параболы, заключенная между точкам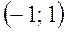и 
и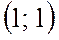 
. Здесь 
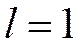, поэтому:
, 
.
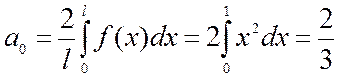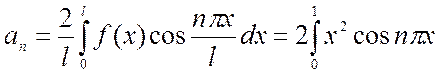Здесь следует дважды интегрировать по частям:
1) 
, 
, 
, 
,
;
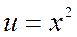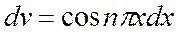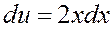2) 
, 
, 
, 
,
.
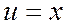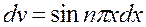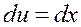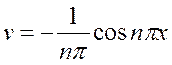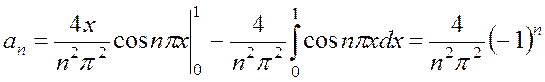Так как рассматриваемая функция – четная, то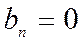 
. Следовательно,
.
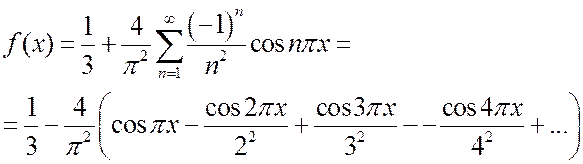