Пример.Найти первые три (отличные от нуля) члена разложения в ряд Маклорена функции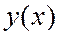 
, являющейся частным решением дифференциального уравнения 
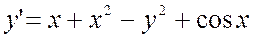, если 
.
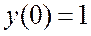Решение.Положим, что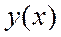 
является решением данного дифференциального уравнения при указанных начальных условиях. Если 
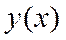допускает разложение в ряд Маклорена, то имеем 
.
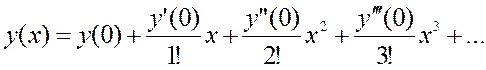Свободный член разложения, т. е.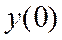 
, дан по условию. Чтобы найти значения 
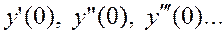, можно данное уравнение последовательно дифференцировать по переменной 
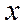и затем вычислить значения производных при величине 
.
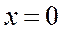Значение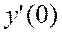 
получаем, подставив начальные условия в данное уравнение: 
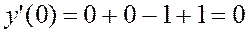, т. е. 
.
,
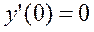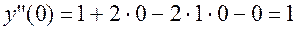, т. е. 
.
,
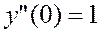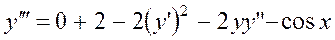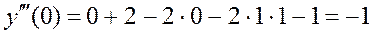, т. е. 
, …
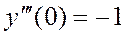Подставив найденные значения производных при значении 
в ряд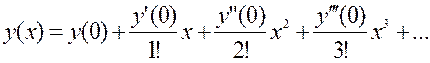 
, получим разложение искомого частного решения уравнения в ряд: 
.
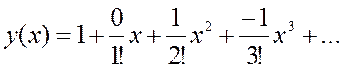Окончательно,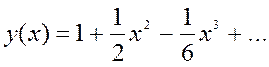 
.
