Задача.Найти приближенное значение функции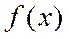 
в точке 
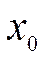с заданной степенью точности 
.
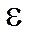Решение.Разложим функцию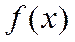 
в ряд по степеням 
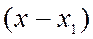с интервалом сходимости, содержащим точку 
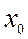, где 
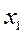– точка, в которой значения функции, а также её производных легко вычисляются, давая точные значения.
Переменной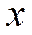 
даем значение 
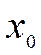и в числовом ряду 
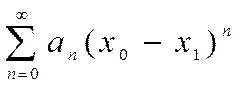оставим только те члены, которые гарантируют заданную точность.
Число таких членов определяется по правилу:
– если ряд знакоположительный, то с помощью остаточного члена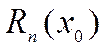 
формулы Тейлора 
, 
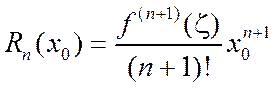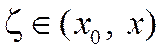
– если ряд знакочередующийся, то с помощью остатка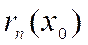 
ряда Тейлора 
.
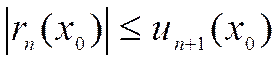Пример.Вычислить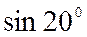 
с точностью 
.
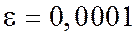Решение.Имеем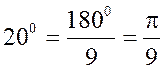 
и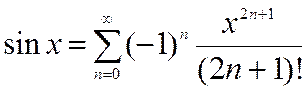 
– знакочередующийся ряд, значит, применим остаток ряда Маклорена.
, 
, 
, 
.
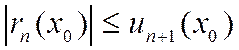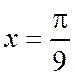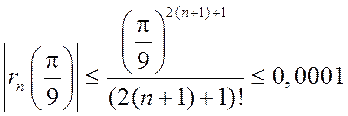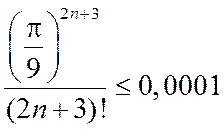Подбором, при значении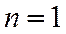 
получим 
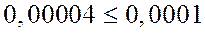– условие выполняется. Тогда, 
.
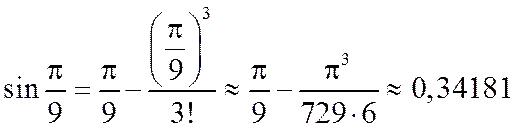Пример.Вычислить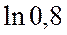 
с точностью 
.
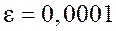Решение.Для вычисления 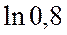запишем ряд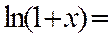 
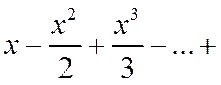
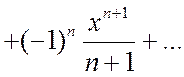. При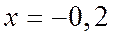 
, входящем в область сходимости ряда 
:
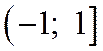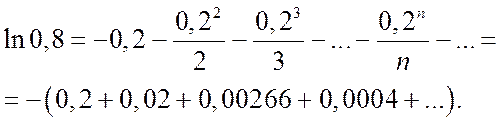
Если в качестве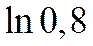 
взять первые четыре члена, мы допустим погрешность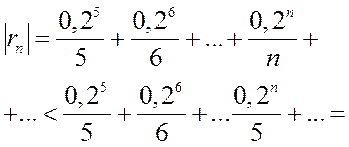 
.
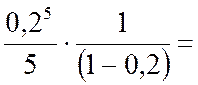
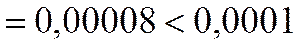Итак,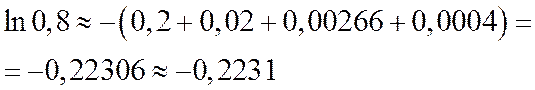 
.
Пример.Вычислить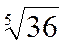 
с точностью 
.
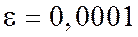Решение.Представим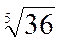 
в виде 
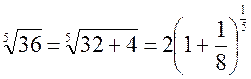. Так как 
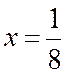входит в область сходимости степенного ряда 
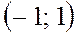, то при значениях 
, 
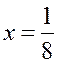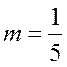, учитывая, что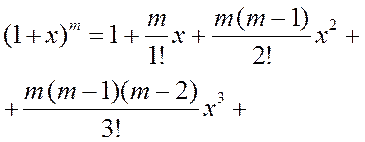 
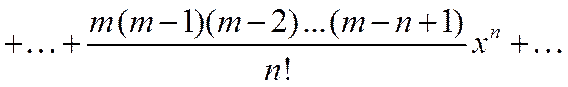, получим:
.
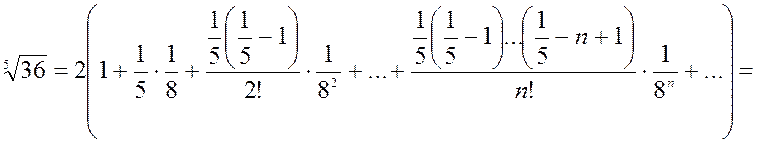
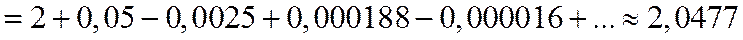Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность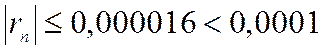 
.
