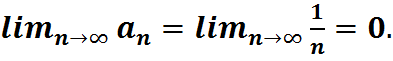Знакочередующиеся ряды

Определение. Если два стоящих рядом члена ряда имеют разные знаки, то ряд называется знакочередующимся. Его вид: .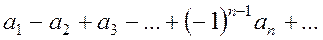

Вопрос о сходимости знакочередующегося ряда решается с помощью следующего признака.

Теорема (признак Лейбница). Если члены знакочередующегося ряда 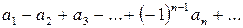удовлетворяют условиям:

1) 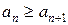, , 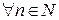т. е. члены ряда не возрастают (убывают) по абсолютной величине;

2) 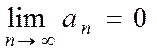, то данный ряд сходится, а его сумма не превосходит первого члена ряда, т. е. .

Пример. Ряд 1- 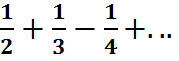сходится, т. к.

1) 1…;

2)