1. На остальные случаи признак сравнения ответа о сходимости ряда не даёт.
2. Этим признаком пользуются, сравнивая данный ряд с рядом сравнения, сходимость которого известна.
Рядами для сравнения являются:
а)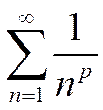 
, 
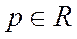– обобщенный гармонический ряд;
– при значении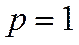 
получаем 
– гармонический ряд, расходится;
– при значении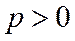 
ряд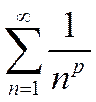 
называется рядом Дирихле. Этот ряд сходится при значении 
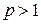и расходится при значении 
;
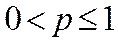– при значении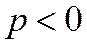 
ряд расходится;
б)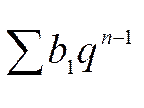 
– геометрический ряд;
– при значении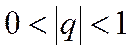 
ряд сходится, при этом его сумма 
;
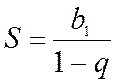– при значении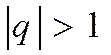 
ряд расходится.
Пример. Исследовать сходимость ряда:
+ 
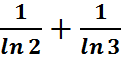+… (1)
; 
; 
;
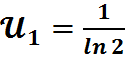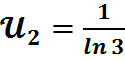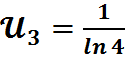Будем сравнивать его с рядом, полученным из гармонического отбрасыванием первого члена
(2)
; 
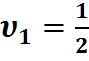Имеем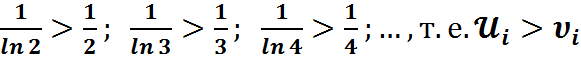 
.
Так как ряд(2) расходится, а члены ряда(1) больше членов ряда(2), то ряд(1) – расходится.
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный ряд»,
но и доказать неравенство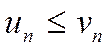 
, для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). В ряде случаев более простым оказывается предельный признак сравнения.
