Примеры числовых рядов:
а)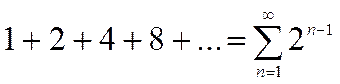 
,
б)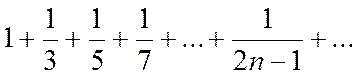 
.
Ряд считается заданным, если известен его общий член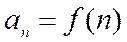 
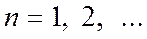, т. е. задана функция 
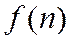натурального аргумента.
Пример. Ряд с общим членом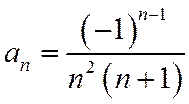 
имеет вид 
.
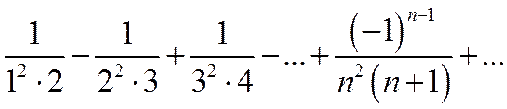Более сложной является задача: по нескольким первым членам ряда составить общий член ряда.
Пример. Найти общий член ряда: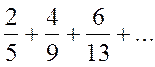 
.
Решение. Заметим закономерности для числителей и знаменателей дробей. Числа 2, 4, 6, … отличаются друг от друга на величину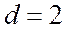 
, т. е. эти числа образуют арифметическую прогрессию с 
. Тогда величину 
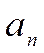определим как общий член арифметической прогрессии 
.
Получим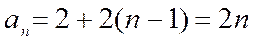 
. Аналогично, числа 5, 9, 13, … образуют арифметическую прогрессию со значениями 
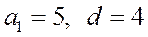. Получим 
.
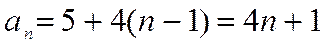В результате для ряда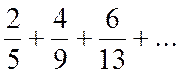 
общий член ряда 
.
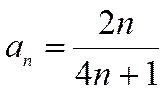Сумма конечного числа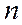 
первых членов ряда (1)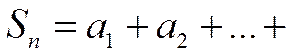 
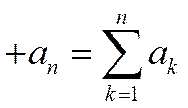называется 
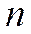-й частичной суммойданного ряда.
Определение.Ряд называется сходящимся, если последовательность его частичных сумм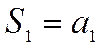 
, 
, 
, …, 
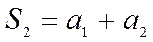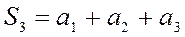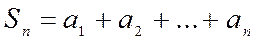при неограниченном возрастании 
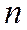имеет конечный предел:
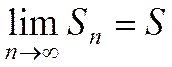. (2)
Этот предел называетсясуммой сходящегося ряда. Если предел не существует или бесконечен, то ряд называется расходящимся.
Ряд, составленный из членов геометрической прогрессии со значениям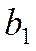и 
и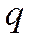 
: 
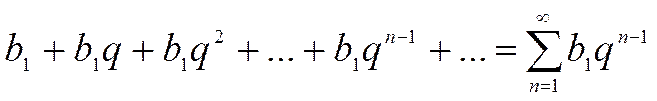называется геометрическим рядом, где 
.
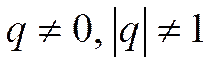Геометрический ряд сходится при величине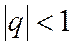 
и расходится при величине 
.
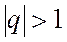