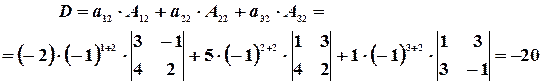Теорема. Определитель каждой матрицы равен сумме произведений элементов любой ее строки (столбца) на их алгебраические дополнения. То есть, при разложении по элементам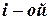 
строки получим:
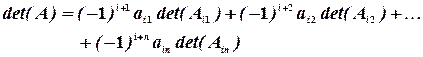
Для вычисления значений определителей матриц второго порядка пользуются формулой:
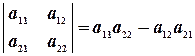
Для вычисления значений определителей матриц третьего порядка можно воспользоваться формулой разложения определителя по первой строке:
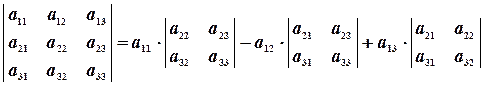
Пример 7.Не вычисляя определителя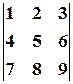 
, показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель
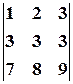, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 
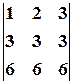, в котором две строки пропорциональны. Такой определитель равен нулю.
Пример 8.Вычислить определитель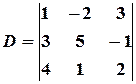 
, разложив его по элементам второго столбца.
Решение. Разложим определитель по элементам второго столбца:
