Дифференциальное уравнение вида
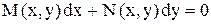(1)
называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции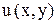 
, т.е.
.
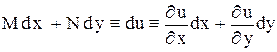Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой области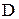 
изменения переменных 
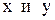выполнялось условие
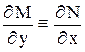(2)
В этом случае общий интеграл имеет вид 
или
.
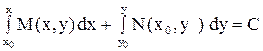Пример 6.
Решить уравнение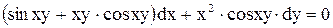 
.
Решение. Проверим является ли данное уравнение уравнением в полных дифференциалах
.
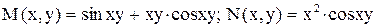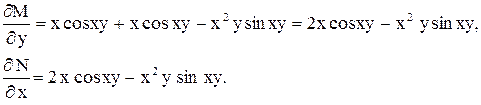
Получили, что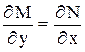 
, условие (2) выполнено, значит данное уравнение в полных дифференциалах.
Найдем функцию 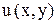. Для этого имеем систему:
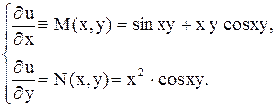
Из первого уравнения, интегрированием по 
при постоянном 
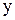, определяем :
,
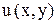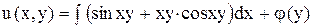где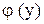 
- произвольная функция (вместо постоянной интегрирования С берем функцию )
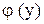Частная производная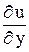 
, найденной функции 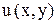должна равняться в силу второго уравнения системы, 
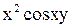, что дает
,
.
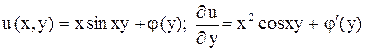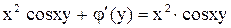Отсюда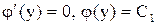 
,
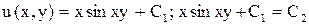- общий интеграл.
Ответ: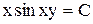 
, где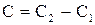 
.
Упражнения. Решить уравнения
1. 
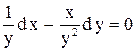. Ответ: 
.
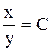2. 
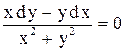. Ответ: 
.
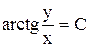3. 
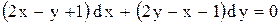. Ответ: 
.
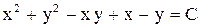4. 
. Ответ: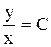 
.
,
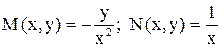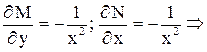уравнение в полных дифференциалах.
Проинтегрировать уравнения в полных дифференциалах:
| 1.
|  .
|
| 2.
|  .
|
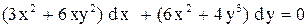| 3.
|  .
|
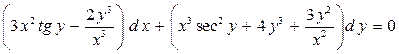| 4.
|  .
|
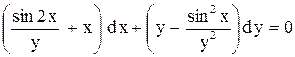| 5.
|  .
|
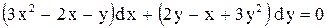| 6.
|  .
|
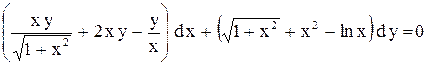| 7.
|  .
|
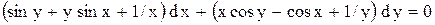| 8.
|  .
|
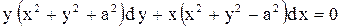| 9.
|  .
|
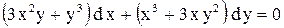| 10.
|  .
|
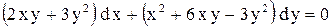| 11.
|  .
|
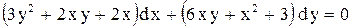| 12.
|  .
|
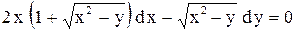| 13.
|  .
|
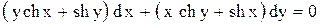| 14.
|  .
|
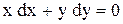| 15.
|  .
|
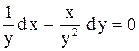| 16.
|  .
|
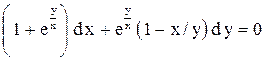| 17.
|  .
|
| 18.
|  .
|
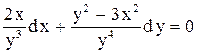| 19.
|  .
|
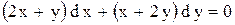| 20.
|  .
|
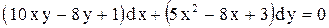| 21.
|  .
|
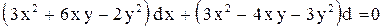| 22.
|  .
|
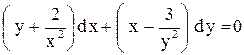| 23.
|  .
|
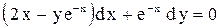| 24.
|  .
|
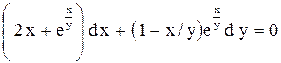| 25.
|  .
|
| 26.
|  .
|
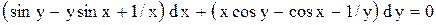| 27.
|  .
|
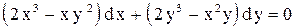| 28.
|  .
|
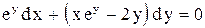| 29.
|  .
|
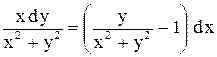| 30.
|  .
|
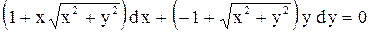