Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А_{m x n} = (a_ij) на матрицу B_{n x p} = (b_jk) называется матрица С_{т х p} = (c_ik) такая, что

c_ik = a_i1 · b_1k + a_i2 · b_2k +…+ a_in · b_nk ( , ).

т. е. элемент i-й строки и k-гостолбца матрицы произведения С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Получение элемента c_ik схематично изображается так:

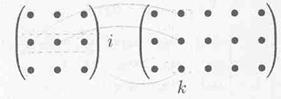
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А · Е = Е · А = А, где А — квадратная матрица, Е — единичная матрица того же размера.

Пример.

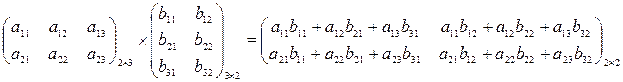
Пример. , . Тогда произведение А В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2).

При этом определено произведение В х А, которое считают следующим образом:

.

· Матрицы А и Вназываются перестановочными,если АВ = ВА.

Умножение матриц обладает следующими свойствами:

1. А·(В·С) = (А·В)·С;

2. А·(В + С) = АВ + АС;

3. (А + В)·С = АС + ВС;

4. α(АВ) = (αА)В,

если, конечно, написанные суммы и произведения матриц имеют смысл.