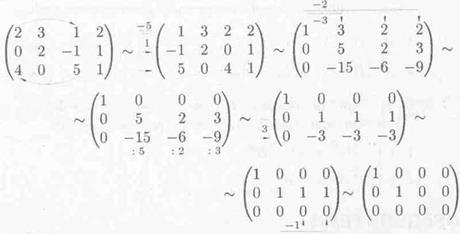Транспонирование

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^Т.

Так, если , то , если 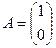, то А^Т = (1 0).

Транспонированная матрица обладает следующим свойством: (А^Т)^Т = А.

Для операции транспонирования верны свойства:

1. (А + В)^Т = А^Т + В^Т;

2. (АВ)^Т = В^Т · А^Т.

Элементарные преобразования матриц

Элементарными преобразованиями матрицявляются:

· перестановка местами двух параллельных рядов матрицы;

· умножение всех элементов ряда матрицы на число, отличное от нуля;

· прибавление ко всем элементам ряда матрицы соответствующих эле­ментов параллельного ряда, умноженных на одно и то же число.

· Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например

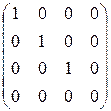
Пример. Привести к каноническому виду матрицу

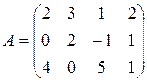
Решение: Выполняя элементарные преобразования, получаем