Определение 20. Векторным произведением векторов 
на вектор 
называется вектор 
, такой, что:
1) его длина равна площади параллелограмма, построенного на векторах и :
;
2) он перпендикулярен каждому из перемножаемых векторов:
;
3) направление вектора определяется по правилу «правой тройки», то есть кратчайший поворот от вектора (первого множителя) к вектору (второму множителю) из конца вектора виден против хода часовой стрелки.
Векторное произведение и обозначается 
.
Если известны координаты векторов:
, 
,
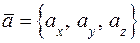то векторное произведение вычисляется по формулам:
,
.
