Направление вектора в пространстве можно задать углами 
, 
и 
, которые составляет данный вектор с осями координат. Косинусы этих углов: 
, 
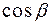и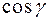 
называются направляющими косинусами вектора.
Рис. 23
Пусть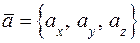 
– произвольный вектор. Согласно формуле проекции вектора на ось будем иметь
,
,
.
Отсюда получим значения направляющих косинусов:
или
,
,
.
Из полученных равенств вытекает следующее тождество
.
Полученное тождество означает, что среди углов , и независимыми являются только два, а третий определяется из тождества (с точностью до знака).
