Определение 8. Разностью 
векторов 
и 
называется вектор, сумма которого с вектором равна вектору . Разность можно определить как сумму вектора с вектором, противоположным к вектору : 
.
Разность векторов и можно вычислить по правилу параллелограмма, как диагональ этого параллелограмма, исходящей из конца вектора (рис. 11).
Сумма и разность векторов определялись по правилу параллелограмма. Можно эти две операции определить по правилу треугольника. Для определения суммы 
, следует параллельным переносом начало вектора совмещать с концом вектора . Для определения разности , следует концы этих векторов.
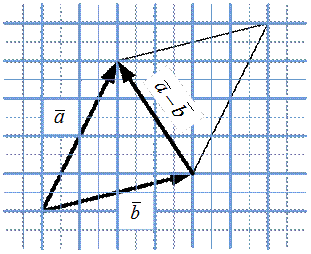
Рис. 11
