Определение 6. Произведением вектора 
на вещественное число 
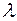называется вектор 
, коллинеарный вектору , имеющий длину 
и сонаправленный с вектором , если 
, и противонаправленный с вектором , если 
. Произведением вектора на число 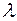обозначается 
или 
.
На рис. 6 – рис. 9 показаны пары векторы и 
, и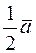 
, и 
, и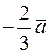 
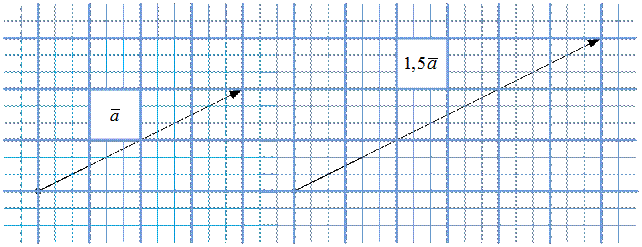
Рис. 3. Случай 
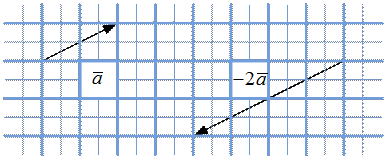
Рис. 4. Случай 
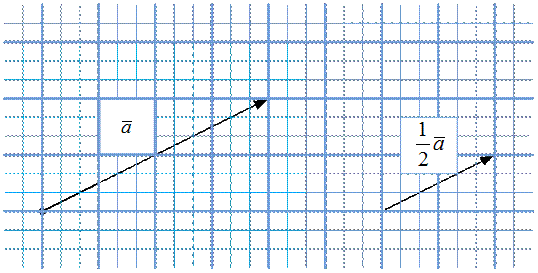
Рис. 5. Случай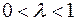 
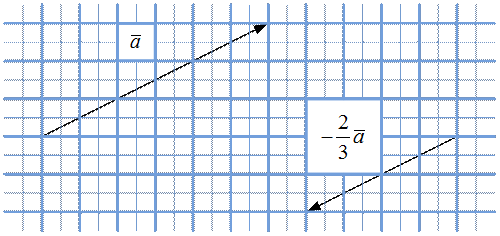
Рис. 6. Случай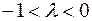 
Противоположный вектор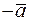 
можно рассматривать как результат умножения вектора на число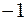 
:
.
Отметим некоторые свойства умножения вектора на число.
1. 
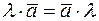– закон коммутативности.
2. 
– закон ассоциативности.
3. 
– закон дистрибутивности.
4. 
– закон дистрибутивности.
Теорема 1. Для коллинеарности векторов и 
, необходимо и достаточно существование числа 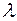такого, что выполняется хотя бы одно из равенств 
или 
.
