Определение 1. Числовой ряд вида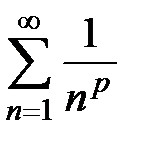 
называется рядом Дирихле с показателем р, 
R. Заметим, что при 
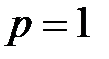получаем ряд 
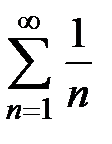, который называется гармоническим.
Пример 1. Исследовать ряд Дирихле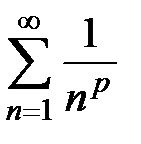 
на сходимость в зависимости от р.
Решение. 1) В случае, если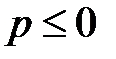 
, члены ряда 
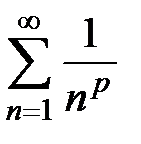образуют неубывающую последовательность, а сам ряд расходится по необходимому признаку сходимости ( 
).
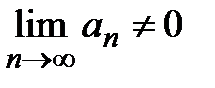2) В случае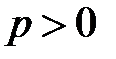 
для исследования сходимости ряда используем интегральный признак Коши. Введём функцию 
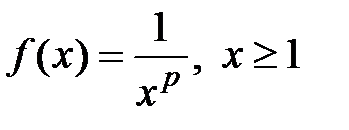, которая удовлетворяет всем условиям теоремы Коши (теорема 3, лекция 1, разд. 1.5): при 
она непрерывна, положительна и монотонно убывает,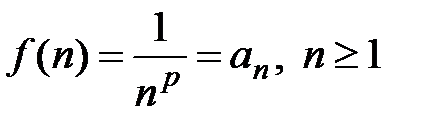 
. Вычислим несобственный интеграл 
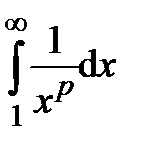в двух случаях а) 
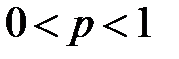, б)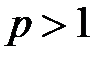 
, т.е. когда 
: 
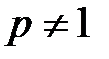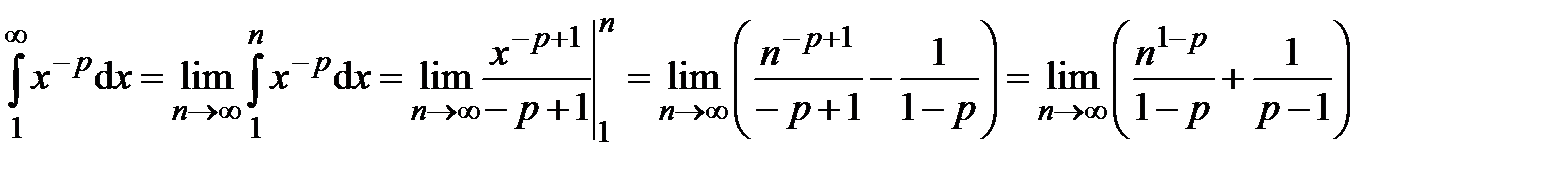
–Если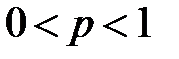 
, 
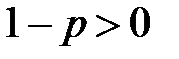, то 
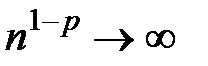при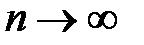 
, тогда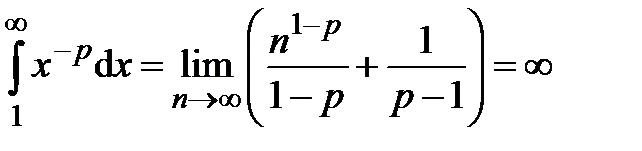 
, следовательно, несобственный интеграл расходится и расходится исходный ряд.
–Если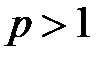 
, 
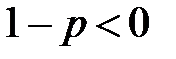, то 
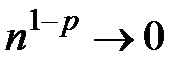при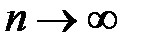 
, тогда 
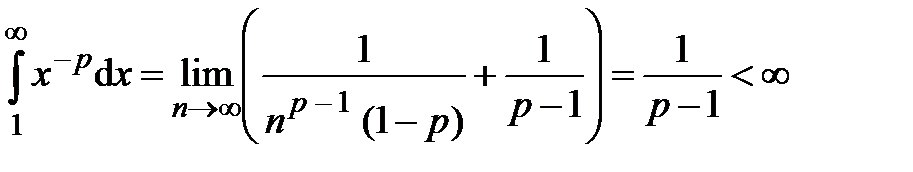, следовательно, несобственный интеграл сходится и сходится исходный ряд.
3) В случае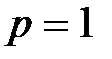 
имеем гармонический ряд 
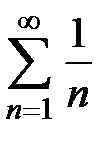, для которого
также применим интегральный признак Коши, т.е. рассмотрим интеграл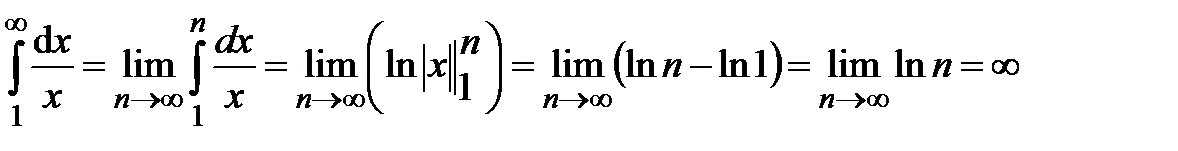 
, следовательно, несобственный интеграл расходится, а значит, гармонический ряд расходится.
Вывод: ряд Дирихле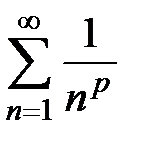 
сходится, если 
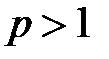, и расходится, если 
.
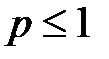