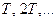1. Четность и нечетность.Функция 
называется четной, если для любых значений 
из области определения 
, и нечетной, если 
. В противном случае функция называется функцией общего вида.
Например, функция 
- четная, так как 
, а функция 
- нечетная, так как 
. В то же время, например, функция 
является общего вида, так как 
и 
, 
.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
2. Монотонность. Функция называется возрастающей (убывающей) на промежутке 
, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 
и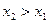 
. Тогда функция возрастает на промежутке , если 
, и убывает, если 
.
3. Ограниченность. Функция называется ограниченной на промежутке , если существует такое положительное число 
, что 
для любого 
. В противном случае функция называется неограниченной.
Например, функция 
ограничена на всей числовой оси, так как 
для любого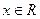 
.
4. Периодичность. Функция называется периодической с периодом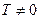 
, если для любых из области определения функций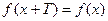 
. Например, функция имеет период (наименьший положительный период) 
, так как для любых значений 
.
График периодической функции может быть получен сдвигом кривой 
вправо (влево) на отрезки 
