Составить канонические уравнения прямой, заданной как линия пересечения двух плоскостей a и b:
|
| a
| b
|
| 1)
| x-2у+2z-8=0
| x+2z-6=0
|
| 2)
| 3x-5y+z-8=0
| 2x+y-z+2=0
|
| 3)
| x-2y+3z-4=0
| 3x+2y-5z-4=0
|
| 4)
| x+z-6=0
| x+6y-4=0
|
| 5)
| x+2y-4=0
| x-2y+2z-8=0
|
| 6)
| x+2Z-6=0
| x+y+z-6=0
|
| 7)
| x+2y+3z-13=0
| 3x+y+4z-14=0
|
| 8)
| x+2y+3z-1=0
| 2x-3y+2z-9=0
|
| 9)
| 2x+7y-z-8=0
| Х+2y+z-4=0
|
Составить канонические уравнения прямой, проходящей через точку А параллельно прямой ℓ:
|
| А
| ℓ
|
| 10.
| (3;1;-1)
| X+5y+2=0
3х+4y+2z-8=0
|
| 11.
| (2;0;-3)
| 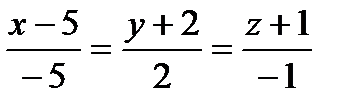
|
| 12.
| (-4;3;0)
| x-2y+z-4=0
2x+y-z=0
|
| 13.
| (2;-5;9)
| 2x-3y-3z-9=0
x-2y+3=0
|
Составить канонические уравнения прямой, проходящей через точку А перпендикулярно прямым ℓ1 и ℓ2:
|
| А
| ℓ1
| ℓ2
|
| 14.
| (2;-3;4)
| 
| 
|
|
| (0;1;1)
| 
| 
|
| 16.
| (2;-3;4)
| x=t;y=t;z=2t+5
| x=3t+8;y=2t-4;z=t+2
|
| 17.
| (0;1;-1)
| x=3t+1;y=15t;z=7t-2
| x=t;y=2t-5;z=6
|
| 18.
| (0;-1;1)
| x=2t;y=t-5;z=3t-2
| x=4t-1;y=4t+6;z=t-4
|
Составить канонические уравнения прямой, проходящей через точки а1 и а2 :
|
| а1
| а2
|
| 19.
| (1;-2;1)
| (3;1;1)
|
| 20.
| (1;-2;1)
| (0;6;5)
|
| 21.
| (3;1;2)
| (0;2;5)
|
| 22.
| (0;1;2)
| (5;2;1)
|
| 23.
| (1;7;3)
| (0;2;1)
|
| 24.
| (1;0;2)
| (5;1;4)
|
| 25.
| (3;5;1)
| (2;3;1)
|