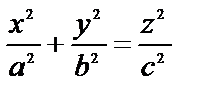(8.12.) – называется уравненим конуса второго порядка. Применив метод сечения получим (Рис.8.13.)
Замечание: Уравнения 
и 
также определяют конус второго порядка.
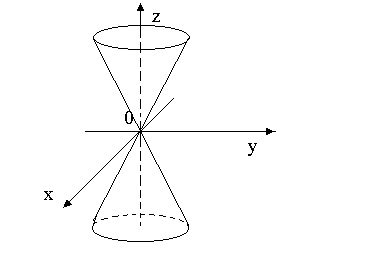
Рис.8.13.
Пример 8.4.4.1. Определить вид поверхности: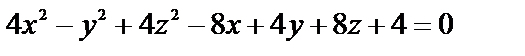 
Решение: Приведем к каноническому виду: 
Произведем параллельный перенос осей координат в точку (1,2,-1):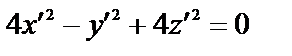 
- коническая поверхность.
Контрольные вопросы и задания.
1. Что называется поверхностью вращения?
2. В чем заключается метод сечения?
3. Запишите канонические уравнения поверхностей второго порядка.
4. Составить уравнение поверхности, образованной вращением эллипса 
вокруг оси Ox .
5. Составить уравнение поверхности, образованной вращением гиперболы 
вокруг оси Oz .
6. Доказать, что эллиптический параболоид, определяемый уравнением 
, может быть получен в результате вращения параболы 
вокруг оси Oz и последующего равномерного сжатия пространства к плоскости Oxz.
7. Доказать, что уравнение z=xy определяет гиперболический параболоид.
8. Доказать, что уравнение 
определяет конус с вершиной в начале координат.
9. Ось Oyявляется осью круглого конуса с вершиной в начале координат; его образующие наклонены под углом в 60° к оси Oy. Составить уравнение этого конуса.
10. Составить уравнение конуса с вершиной в точке S(3;0;-1), образующие которого касаются эллипсоида 
.
