Определение. Гиперболический параболоид - поверхность, каноническое уравнение которой имеет вид 
(8.9.) где pq > 0.
Исследуем форму этого параболоида при p > 0, q > 0.
Пусть y=0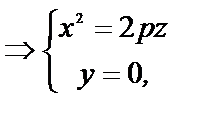 
(8.10.)- парабола в плоскости zox.
Пусть x=0 
(8.11.) - парабола, обращенная ветвями вниз в плоскости zoy.
Пересечем поверхность плоскостями x=h, x=-h:
или 
- параболы с ветвями вниз и вершинами, поднятыми вверх над осью Ох на 
.
- пара пересекающихся прямых (проходящих через т.О),с угловыми коэффициентами: 
: 
.
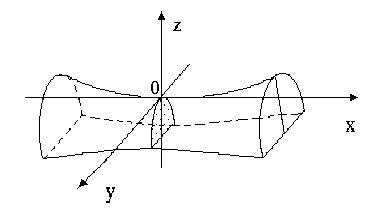
Рис.8.12.
В силу произвольного 
заключаем, что гиперболический параболоид может быть образован путем параллельного перемещения параболы (8.11.), при котором её вершина движется по параболе (8.10.).
Если z = -m < 0;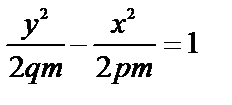 
, получим гиперболу с действительной полуосью 
.
При z = l > 0; 
, гипербола с действительной полуосью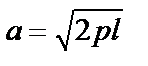 
. Полученные сечения позволяют построить искомую поверхность (Рис.8.12.).
Пример 8.4.3.1. Определить вид поверхности: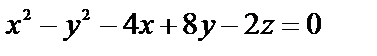 
Решение: Приведем к каноническому виду: 
Произведем параллельный перенос осей координат в точку (2,4,6): 
- гиперболический параболоид.
